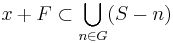Piecewise syndetic set

In mathematics, piecewise syndeticity is a notion of largeness of subsets of the natural numbers.

Let 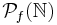$\mathcal{P}_f(\mathbb{N})$ denote the set of finite subsets of 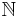$\mathbb{N}$ . Then a set 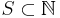$S \sub \mathbb{N}$ is called piecewise syndetic if there exists 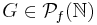$G \in \mathcal{P}_f(\mathbb{N})$ such that for every 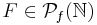$F \in \mathcal{P}_f(\mathbb{N})$ there exists an 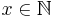$x \in \mathbb{N}$ such that

$x%2BF \subset \bigcup_{n \in G} (S-n)$

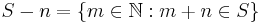where $S-n = \{m \in \mathbb{N}: m%2Bn \in S \}$ . Informally, S is piecewise syndetic if S contains arbitrarily long intervals with gaps bounded by some fixed bound b.

1 Properties
2 Other Notions of Largeness
3 See also
4 Notes
5 References

Properties

A set is piecewise syndetic if and only if it is the intersection of a syndetic set and a thick set.

If S is piecewise syndetic then S contains arbitrarily long arithmetic progressions.

A set S is piecewise syndetic if and only if there exists some ultrafilter U which contains S and U is in the smallest two-sided ideal of $\beta \mathbb{N}$ , the Stone–Čech compactification of the natural numbers.

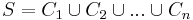Partition regularity: if $S$ is piecewise syndetic and $S = C_1 \cup C_2 \cup ... \cup C_n$ , then for some 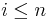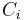$i \leq n$ , $C_i$ contains a piecewise syndetic set. (Brown, 1968)

If A and B are subsets of 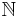$\mathbb{N}$ , and A and B have positive upper Banach density, then 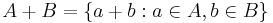$A%2BB=\{a%2Bb:a \in A, b \in B\}$ is piecewise syndetic^[1]

Other Notions of Largeness

There are many alternative definitions of largeness that also usefully distinguish subsets of natural numbers:

cofinite
positive upper density
syndetic
thick
member of a nonprincipal ultrafilter
IP set

Notes

^ R. Jin, Nonstandard Methods For Upper Banach Density Problems, Journal of Number Theory 91, (2001), 20-38</math>.

References

J. McLeod, "Some Notions of Size in Partial Semigroups" Topology Proceedings 25 (2000), 317-332
Vitaly Bergelson, "Minimal Idempotents and Ergodic Ramsey Theory", Topics in Dynamics and Ergodic Theory 8-39, London Math. Soc. Lecture Note Series 310, Cambridge Univ. Press, Cambridge, (2003)
Vitaly Bergelson, N. Hindman, "Partition regular structures contained in large sets are abundant", J. Comb. Theory (Series A) 93 (2001), 18-36
T. Brown, "An interesting combinatorial method in the theory of locally finite semigroups", Pacific J. Math. 36, no. 2 (1971), 285–289.

Piecewise syndetic set

Contents

Properties

Other Notions of Largeness

See also

Notes

References